An Accurate, Inexpensive Attitude Determination and Control System for CubeSats by Duarte Rondão, Cass Hussmann and Afzal Suleman Part 6
From The Space Library
Contents |
VI. Numerical Simulations
In this section, the performance of the proposed attitude determination system is investigated. The attitude control system has not yet been simulated. The truth model dynamics are ruled by Eqs. (II.9) and (II.16), as presented in Section II. Table 6 displays the general model parameters used for the simulation. In addition, uncalibrated attitude sensors were also modeled, in accordance with Section V. In particular, the rate gyro is modeled with ARW and RRW induced noise, misorientation, misleveling, scaling and quantization errors; the magnetometer is modeled with noise, static bias, misorientation, misleveling, scaling and quantization errors; and the sun sensor is modeled with noise and quantization errors. All sensors are sampled at 10 Hz. Spacecraft disturbance torques were also modeled, namely aerodynamic, radiation pressure, gravity gradient and magnetic disturbance torques. For Cases 1 and 2, the performance of the four estimation algorithms presented in Section III is benchmarked. For Case 3, the nominal estimation method chosen based on the results of Cases 1 and 2 is evaluated.
A. Case 1
Consider that the spacecraft is spinning at the constant angular rate for the nadir-tracking of the orbit characterized in Table 6, i.e.,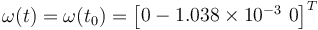 
rad s-1. The true initial attitude for this scenario is 
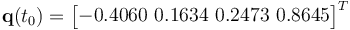. The initial unknown bias of the rate gyro is 
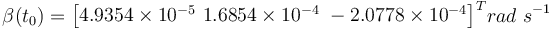. The estimated initial quaternion to initialize the four algorithms is chosen such that it represents an angular error of 90 deg with respect to the truth value. The estimated initial bias is chosen such that it represents an error in magnitude of 50 deg h − 1 . This is done to test the convergence properties of the filters under large initial errors.
For MEKF, UQKF and 2STEP, the process noise parameters are input as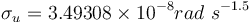 
Table 5: RWS characteristics for individual flywheel/motor. [18]
Table 6: General model parameters.
and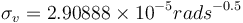 
. The measurement noise standard deviations are 
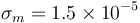for the magnetometer and 
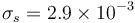for the sun sensor. For MEKF and UQKF, the initial covariance 
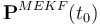matrix is 
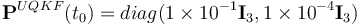, where diag 
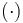denotes a diagonal matrix of appropriate dimension. This is proportional to the magnitude of the initial errors, being high enough so as not to give the filters too much confidence in the initial estimates, but also low enough that they are not considered too far off from the truth values. 2STEP is an exception to this, being initialized with 
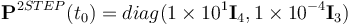where a lower covariance matrix for the quaternion would compromise the robustness of the filter. For UQKF, 
was set. The gains for GEOB were set up as 
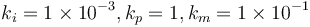and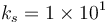 
.
Results are plotted in Figure 4 for the duration of five orbits. The grey areas represent eclipse periods where the sun sensor measurement is unavailable. Despite large initial errors, all algorithms are able to immediately reduce it in at least one-tenth of its value. 2STEP and GEOB converge the fastest, followed by MEKF, which achieves a 2 deg error after 1.5 orbits. UQKF takes about the same time to converge as MEKF, but yields larger errors before doing so. After convergence, MEKF and UQKF have the best overall performance, with the angular error rounding 1.5 deg during eclipse and achieving an accuracy up to a tenth of degree outside eclipse. GEOB is the least robust in the long run, as the error spikes during eclipse periods. Also, it can be seen that it exhibits periodic error spikes outside of eclipse at t = 0.75, 1.75, 2.75,... orbits. These correspond to points in the orbit where the sun sensor and magnetometer measurements approach collinearity. The algorithm is quite sensitive to these perturbations in the beginning of the simulation; as time progresses, these spikes are increasingly mitigated.
Figure 4: Performance of the attitude estimation algorithms for Case 1.
B. Case 2
Case 2 includes the same orbital conditions and filter parameters as Case 1. Now, however, convergence from extreme error cases is tested. The estimated initial quaternion to initialize algorithms is chosen such that it represents an angular error of 180 deg with respect to the truth value. The estimated initial bias is chosen such that it represents an error in magnitude of 100 deg h-1 . The initial covariance matrix for MEKF and UQKF is set as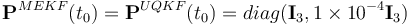 
and for 2STEP as 
.
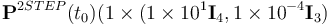Results are plotted in Figure 5. A logarithmic scale for the y−axis is employed to depict the high error magnitudes. MEKF is only able to achieve convergence after more than 3.5, while UQKF is able to do so in under 2.5 orbits. 2STEP is not able to achieve convergence. Note that the value for the quaternion error covariance in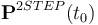 
was the maximum possible value without leading to numerical instability. The large initial angular error causes GEOB to reach an angular error of almost 100 deg during the first eclipse. However, for the rest of the run, the algorithm’s performance is comparable to the one in Case 1. Most notably, like in the previous case, the algorithm is able to converge almost immediately.
C. Case 3
The convergence properties observed in Cases 1 and 2 for GEOB and the steady-state performance characteristics and computational lightness of MEKF with respect to UQKF and 2STEP lead to a third case study where a hybrid of these two algorithms is implemented. The orbital conditions and filter parameters are the same as in Cases 1 and 2. The estimated initial quaternion and bias represent errors of 180 deg and 100 deg h-1 in magnitude, respectively. Here, the attitude acquisition is performed with GEOB. At t = 600 s, still before the first eclipse, the attitude estimator switches to MEKF for the rest of the run. When the switch occurs, MEKF is initialized with the last quaternion and bias estimates provided by GEOB and with a covariance matrix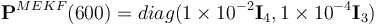 
.
Results are plotted in Figure 6. The algorithm shows almost instantaneous convergence.
