An Accurate, Inexpensive Attitude Determination and Control System for CubeSats by Duarte Rondão, Cass Hussmann and Afzal Suleman Part 2

From The Space Library

Revision as of 15:42, 8 November 2016 by DRondao (Talk | contribs)
(diff) ←Older revision | Current revision (diff) | Newer revision→ (diff)
Jump to: navigation, search

II. Preliminaries

A. Reference Frames

The reference frames used are summarized:

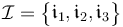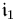  • Earth-Centered-Inertial (ECI) Frame: designated by \mathcal {I} = \begin{Bmatrix} \mathfrak {i}_1, \mathfrak {i}_2, \mathfrak {i}_3\end{Bmatrix}The \mathfrak {i}_1 axis is aligned with the vernal equinox direction, the 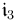\mathfrak {i}_3 axis is aligned with the Earth’s North pole, and the 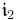\mathfrak {i}_2 axis completes the right-handed triad. Since neither the polar axis nor the vernal equinox direction are inertially fixed, the ECI axes are defined to be mean orientations at a fixed epoch time [1]. The used epoch is the current standard epoch, J2000.
  • Local-Vertical/Local-Horizontal (LVLH) Frame: designated by 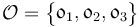\mathcal {O} = \begin{Bmatrix} \mathfrak {0}_1, \mathfrak {0}_2, \mathfrak {0}_3\end{Bmatrix}. Also denoted by the orbital reference frame. It is especially convenient for Earth-pointing spacecraft (SC), being attached to its orbit. 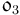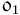The \mathfrak {0}_3 axis points along the nadir vector towards the center of the Earth, the \mathfrak {0}_2 axis is aligned with the negative orbit normal, and the \mathfrak {0}_1 axis completes the right-handed system.
  • Body Frame: designated by 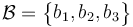\mathcal {B} = \begin{Bmatrix} b_1, b_2, b_3\end{Bmatrix}. The origin of the frame is typically fixed at the center of mass of the spacecraft and the axes rotate with it. The conventioned orientation depends on the spacecraft manufacturer. In the case of ECOSat-III, the 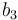\ {b}_3 axis points in the direction of the hyperspectral camera’s field-of-view, the 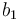\ {b}_1 is aligned with the normal of the bottom plate adjacent to the antenna, and 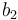\ {b}_2 completes the right-handed system (see Figure 1).

B. Attitude Kinematics

Quaternions provide a quite useful parameterization of the attitude [2]. They are more compact that the direction cosine matrix, requiring only four parameters instead of nine, and they are free from singularities. As it is common practice in spacecraft attitude determination and control applications, this paper uses the JPL quaternion convention [3]. The quaternion is thus defined as

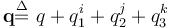\textbf{q}\overset{\Delta}{=} \ q + q_1^i + q_2^j + q_3^k (II.1)

where 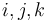\ i, j, k are hypercomplex numbers that satisfy

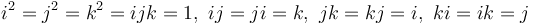i^2 = j^2 = k^2 = −ijk = −1, \ −ij = ji = k, \ −jk = kj = i, \ −ki = ik = j (II.2)

The quantity \ q is the real or scalar part of the quaternion and \ q_1i + q_2j + q_3k is the imaginary or vector part. When subjected to a unit norm constraint, the quaternion becomes a quaternion of rotation [4]. It can be represented as a four-dimensional column matrix:

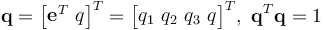\textbf{q} =\begin{bmatrix} \textbf{e}^T \ q \end{bmatrix}^T = \begin{bmatrix} q_1\ q_2 \ q_3\ q\end{bmatrix}^T, \ \textbf{q}^T \textbf{q} = 1 (II.3)

Since four parameters are used to describe the three-dimensional attitude, the quaternion components cannot be independent of each other and the constraint given in Eq. (II.3) must be included [5]. Henceforth, whenever a quaternion is mentioned, it is implied to be a quaternion of rotation, which can thus be done without loss of generality.

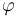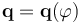A useful expression for the quaternion comes from the fact that it can be parameterized by a three-dimensional vector \ \varphi such \textbf{q} = \textbf{q}(\varphi). For small rotations, such parameterization can be approximated by half angles:

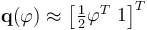\textbf{q}(\varphi) \approx \begin{bmatrix}\frac{1}{2} \varphi^T \ 1\end{bmatrix}^T (II.4)

Another advantage of the quaternion is that the direction cosine matrix, 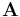\textbf{A}, that transforms the ECI frame to the body frame can be expressed as a quadratic function of the elements of 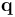\textbf {q}, evading the use of transcendental functions:

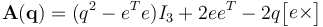\textbf{A}(\textbf{q}) = (q^2 - e^Te) I_3 + 2ee^T - 2q \begin{bmatrix}e\times \end{bmatrix}, (II.5)

where 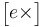\begin{bmatrix}e\times \end{bmatrix}is the cross-product matrix defined by

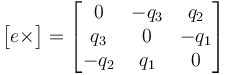\begin{bmatrix}e\times\end{bmatrix}= \begin{bmatrix}0&-q_3&q_2\\q_3&0&-q_1\\-q_2&q_1&0\end{bmatrix} (II.6)


The product between two quaternions 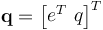\textbf{q} =\begin{bmatrix}e^T \ q \end{bmatrix}^T and \textbf{q}^\prime =\begin{bmatrix}e^{\prime T} \ q^\prime \end{bmatrix}^T given by

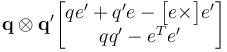\textbf{q} \otimes \textbf{q}^\prime \begin{bmatrix}qe^\prime + q^\prime e-\begin{bmatrix}e\times\end{bmatrix} e ^\prime \\ qq^\prime - e^Te^\prime\end{bmatrix} (II.7)

The quaternion inverse is denoted as

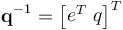\textbf{q}^{-1} = \begin{bmatrix}−e^T \ q\end{bmatrix}^T (II.8)

Note that 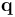\textbf{q} and -\textbf{q} represent the same rotation. The kinematics equation is linear in the quaternion:

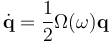\dot \textbf{q} = \frac{1}{2} \Omega ( \omega ) \textbf{q} (II.9)

where \mathbf {\omega} = \begin{bmatrix}\omega_1 \ \omega_2 \ \omega_3\end{bmatrix}^T is the three-element angular rate and

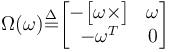\Omega(\omega) \overset{\Delta}{=}\begin{bmatrix}- \begin{bmatrix}\omega \times \end{bmatrix}&\omega\\- \omega^T&0\end{bmatrix} (II.10)

A rate gyro is a typical sensor used in attitude determination and control to measure 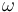\ \omega. A simple model for a rate gyro is given by [5,6]:

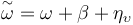\overset\sim{\omega} = \omega + \beta + \eta_\upsilon (II.11a)

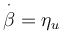\overset\cdot{\beta} = \eta_u (II.11b)

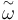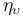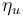Here, \overset\sim{\omega} is the angular velocity as measured by the gyro, \ \beta is the bias, or drift, and \ \eta_\upsilon and \ \eta_u are zero-mean Gaussian white noise variables that satisfy

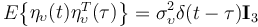E \begin{Bmatrix} \eta_\upsilon(t)\eta_\upsilon^T( \tau) \end{Bmatrix} = \sigma_\upsilon^2 \delta(t- \tau)\textbf{I}_3 (II.12a)

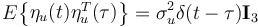E \begin{Bmatrix} \eta_u(t)\eta_u^T( \tau) \end{Bmatrix} = \sigma_u^2 \delta(t- \tau) \textbf{I}_3 (II.12b)

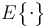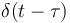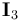where E \begin{Bmatrix}\cdot \end{Bmatrix} is the expectation operator, \ \delta (t - \tau) is the Diract delta function, \sigma_{\upsilon,u}^2 are the noise variances and \textbf{I}_3 is the 3 × 3 identity matrix.

Please continue to Part 3 here

Retrieved from "http://www.thespacelibrary.com/mediawiki/index.php/An_Accurate%2C_Inexpensive_Attitude_Determination_and_Control_System_for_CubeSats_by_Duarte_Rond%C3%A3o%2C_Cass_Hussmann_and_Afzal_Suleman_Part_2"